Programación Orientada a Restricciones

PROGRAMACIÓN
ORIENTADA A
RESTRICCIONES

“Un mundo sin restricciones sería totalmente caótico”. “Que algo es predecible implica que existe una restricción”. “Cada ley de la naturaleza es una restricción” (William Ross Ashby)

“Las leyes describen restricciones; no crean”. “El universo está basado en la libertad. Las leyes, restricciones sobre la libertad, son secundarias” (Arthur M. Young)

Sistema Orientado a Restricciones
En un sistema orientado a restricciones, el usuario define (mediante un lenguaje específico) el espacio de soluciones de un problema, suministra las restricciones que existen y especifica el tipo de solución buscada. El sistema, automáticamente, mediante un motor de búsqueda, trata de encontrar la solución.

En teoría, un sistema de este tipo se aproxima al ideal de la programación automática, pues se utiliza una programación meramente declarativa y libera al programador de tener que desarrollar un algoritmo de búsqueda para cada problema. Pero hay dificultades en la práctica:

No existe un sistema orientado a restricciones universal (general problem solver). Lo normal es limitarse a un dominio específico.
Muchos problemas no se pueden especificar solamente en forma de restricciones. Normalmente se requiere el acudir a otros paradigmas de programación adicionales.
La especificación de un sistema de este tipo requiere un análisis profundo para definir con claridad el espacio de soluciones, las restricciones y la solución a buscar.
Puede ocurrir que los recursos necesarios (tiempo y memoria) para encontrar las soluciones sean desproporcionados, si los motores de búsqueda realizan búsquedas exhaustivas.

Pero el paradigma de restricciones también proporciona ventajas:

Si no se dispone de ningún sistema para implementar restricciones, el análisis del problema con esta filosofía ayuda a su especificación y a la programación.
Si se dispone de un sistema para implementar restricciones, puede ser una buena herramienta para crear prototipos.

Especificación en MENTAL
Con MENTAL no se necesita ningún lenguaje particular para especificar un Sistema Orientado a Restricciones. Bastan los propios recursos del lenguaje.

Un problema típico de la Programación Orientada a Restricciones consiste en buscar los valores de una serie de variables desconocidas que deben cumplir una serie de condiciones (restricciones) que deben de satisfacer a la vez. En el caso de que la expresión condicional sea muy extensa, se pueden utilizar representaciones (sustituciones potenciales) para mejorar la comprensión.

Ejemplo

Un ejemplo clásico es el “problema de las 8 reinas”. Propuesto por el ajedrecista Max Bezzel en 1848, se trata de encontrar una posición en el tablero de ajedrez con las siguientes restricciones: 1) hay solo 8 reinas en el tablero, y 2) ninguna reina puede atacar a otra reina.

Una de las soluciones del
problema de las 8 reinas

Hay 92 soluciones posibles, de las cuales 12 son esencialmente distintas, pues el resto se obtienen por simetrías, rotaciones y traslaciones.

Este problema (que es NP-Completo) interesó a matemáticos como Gauss y Cantor, que lo generalizaron a n reinas sobre un tablero de n×n casillas.

Numerando las filas de abajo-arriba, y las columnas de izquierda a derecha, y representando las posiciones de las reinas mediante la secuencia (i1 … i8), en donde ij es la columna ocupada por la reina de la fila j, la expresión de la solución, junto con las restricciones, es la siguiente:


s = {⟨([i[1…8]]) ← ij≠ik ← j≠k ← (abs(ij−ik) ≠ abs(j−k)) 

← j≥1 ← j≤8 ← k≥1 ← k≤8 ⟩}

Una solución (la indicada en la imagen) es: (2 4 5 8 3 1 7 5).

La condición ij≠ik ← j≠k es la no pertenencia a la misma fila.
La condición abs(ij−ik) ≠ abs(j−k) es la no pertenencia a la misma diagonal. Cuando dos reinas están en una misma diagonal, la diferencia (en valor absoluto) entre sus respectivas filas es igual a la diferencia (en valor absoluto) entre sus respectivas columnas.
abs es el valor absoluto de un número entero:

⟨( abs(m) = (−m ← m<0 →' m) )⟩ // m indica número entero

Su generalización para n reinas es:


⟨( s(n) = {⟨([i⌊1…n⌋]) ← ij≠ik ← j≠k ← (abs(ij−ik) ≠ abs(j−k)) 
                 ← j≥1 ← j≤n ← k≥1 ← k≤n ⟩} )⟩

Este problema no tiene solución para n=2 y n=3.

Para n=4 tiene una única solución: (2 4 1 3).

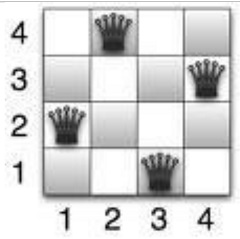
La única solución del
problema de las 4 reinas

Para mejorar la comprensión, podemos utilizar expresiones auxiliares. Por ejemplo:


( CondCol =: (ij≠ik ← j≠k) )  // condición de distinta columna



( CondDiag =: (abs(ij−ik) ≠ abs(j−k)) )  // condición de distinta diagonal



( CondGen =: (j≥1 ← j≤n ← k≥1 ← k≤n) )  // condición general

Y la expresión general sería:


⟨( s(n) = {⟨([i⌊1…n⌋]) ← CondCol ← CondDiag ← CondGen⟩} )⟩

Adenda
Un poco de historia

El pionero de la Programación Orientada a Restricciones (Constraint-Oriented Programming) fue Ivan Sutherland [1963], que en su tesis describía Sketchpad, un sistema orientado a la generación y edición de figuras geométricas. Sus ideas eran avanzadas para su época y requerían hardware y software que no estaba entonces disponible.
La Programación Orientada a Restricciones empezó con la programación lógica, incluyendo restricciones dentro de un programa lógico. Es por ello que se denominó Programación Lógica Restringida (Constraint Logic Programming, CLP). Fueron Jaffar y Lassez los primeros que la utilizaron en aplicaciones con Prolog II. Las primeras implementaciones de CLP fueron Prolog III, CLP(R) y CHIP. Hoy día, la mayoría de las implementaciones de Prolog incluyen una o más librerías para CLP.
OPS5 y ThingLab son sistemas de propósito general del tipo “condición → acción”, con los que se pueden implementar aplicaciones orientadas a restricciones.
IDEAL es otro sistema que utiliza auto−restricciones para el dibujo de figuras geométricas. Incorpora un resolvedor de ecuaciones.

Bibliografía

Bal, Henri E. y Grune, Dick. Constraint Programming. Apartado 7.1.1 de Programming Language Essentials. Addison−Wesley, 1994.
Krzyztof, R. Principles of Constraint Programming. Cambridge University Press, 2003.
Leler, W. Constraint Programming Languages – Their Specification and Generation. Addison−Wesley, 1988.
Sutherland, Ivan. Sketchpad: A Man−machine Graphical Communication System. Garland Publications, 1963, 1980.